ハノイの塔に挑戦

ハノイの塔はどんな塔

ハノイの塔とその解き方

今回はパズルゲームのハノイの塔をとりあげます。

ハノイの塔は 3 つの棒と、ドーナツ型の大きさの異なる複数の円盤でできています。よく木でできたハノイの塔が売っているのを見たことがある方も多いと思います。

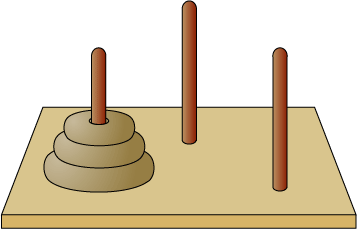図 3-1 ハノイの塔

ハノイの塔は、塔にさしてある円盤を異なる塔に動かすことが目的です。このときに 2 つのルールがあります。

• 一度に一枚しか動かすことができない
• 自分より小さい円盤の上に載せることはできない

たったこれだけのルールですが、なにも事前の知識がないと、結構難しいです。

逆にいうと動作の原理さえ分かれば、円盤の枚数がいくら増えても解き方はまったく同じなので、すぐに解けるはずです。

これ以降はハノイの塔の解法について説明しますが、解き方なんかどうでもいいという方は次の章へと進んでいただいても結構です。

それでは、円盤が 1 枚の時から考えていきましょう。1 枚の時はとても簡単ですね。単に目的の棒に動かすだけですみます。

図 3-2 はハノイの塔を横から見た図です。図では、塔 1 に刺さっている円盤 1 を、塔 2 に移動させています。

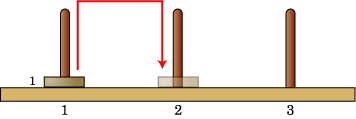図 3-2 1 枚の時の解法

次に 2 枚の時です。基本的な考え方は、小さい円盤は一時退避させておくことです。図 3-3 a) では、まず、円盤 1 を塔 3 に退避させています。こうすれば、b) に示したように、円盤 2 は塔 2 に移動させることができます。

円盤 2 を移動させた後であれば、円盤 1 を塔 2 に動かすことができます。これで、完成です。

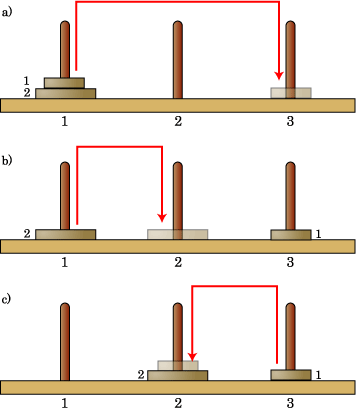図 3-3 2枚の時の解法

それでは 3 枚に挑戦してみましょう。でも、2 枚は動かせるので、その分をはしょっています。まず図 3-4 a) に示したように、円盤 1 と円盤 2 を塔 3 に動かしておきます。これも 2 枚の時と同じように一時退避と考えることができますね。

円盤 3 は上にのっているものがなくなったので、塔 2 に移動することができます。ここで、また、2 枚は動かせるということを利用して、塔 3 から塔 2 へ円盤 1, 2 を動かします。

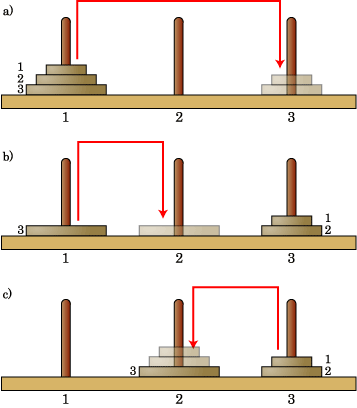図 3-4 3 枚の時の解法

ここまでくると、なんとなく法則性が見えてきませんか。この法則性をはっきりさせるために、円盤が n 枚の時を考えてみましょう。

3 枚の時は、一番大きい円盤を除いた 2 枚を他の塔に移動させることができるということを利用しました。順々に考えていくと、4 枚を移動させるなら、 3 枚なら他の塔に移動できたことを利用できます。これを続けていって、n - 1 枚まで移動させることができたとしましょう。

n 枚の時も、一番大きい円盤を除いた n - 1 枚が動かせるということを利用します。やはり今までと同じように、n - 1 枚を一時的に塔 3 に動かします。

こうすることで、円盤 n を塔 2 に移動させることができます。

残った n - 1 枚を最後に塔 2 に移動させます。

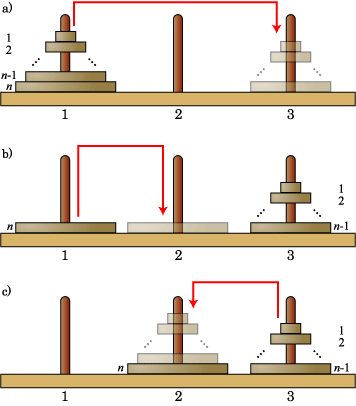図 3-5 n 枚の時の解法

ハノイの塔の解法の法則性は n 枚の時の解き方から次のようにいうことができます。

ここで、解法を示したのはアプリケーションでハノイの塔を解いてみようと思っているからです。ただし、アプリケーションで解くのは後回しにして、まずはプレイヤーに解いてもらうことから始めて見ましょう。

(Nov. 2000)